基于海洋调查实测资料的中尺度涡旋识别结果的验证及边界拟合技术

彭汉帮; 王金虎; 吴克亮; 杨春辉

doi:10.12284/hyxb2021013

基于海洋调查实测资料的中尺度涡旋识别结果的验证及边界拟合技术

doi: 10.12284/hyxb2021013

解放军92192部队，浙江宁波 315122

详细信息

作者简介:
彭汉帮（1990-），男，江西省上饶市人，助理工程师，主要从事海洋水文预报保障。E-mail：824693149@qq.com

中图分类号: P714⁺.1
计量
- 文章访问数: 416
- HTML全文浏览量: 88
- PDF下载量: 57
- 被引次数: 0
出版历程
- 收稿日期: 2019-11-29
- 修回日期: 2020-03-31
- 网络出版日期: 2021-01-27
- 刊出日期: 2021-01-25

Verification and fitting for the results of mesoscale eddy detection based on the observed data

The 92192 Unit of PLA, Ningbo 315122, China

摘要

摘要: 结合卫星高度计资料，本文在海洋中尺度涡旋综合识别法(综合法)的基础上，利用实测资料对识别的涡旋边界和中心点进行比对验证，得出以下结论：(1)通过诊断涡旋识别的边界切线与实测海流矢量的夹角，结果表明综合法识别的涡旋边界形态基本可以反映实测涡旋的水平形态；(2)利用实测海流和温度资料反演涡旋中心，通过与综合法识别的涡旋中心进行比对，结果显示涡旋识别的中心位置与反演的涡旋中心位置基本吻合。此外，通过比对圆与椭圆对识别涡旋的边界拟合效果，结果显示椭圆拟合准确率高于圆拟合准确率。
- 中尺度涡 /
- 涡旋识别 /
- 圆拟合 /
- 椭圆拟合
Abstract: Based on the hybrid detection method for ocean mesoscale eddy, this paper uses the measured data to verify the detected boundary and center of eddy, and draws the following conclusions. (1) By diagnosing the angle between the detected boundary and the measured current vector, the results show that the detected boundary of eddy can basically reflect the current state of the actual eddy. (2) The center of detected eddy is compareed with the center that inversed by the measured current and temperature data. The results show that the detected center of eddy is basically consistent with the inversed center. Furthermore, by comparing the fitting effect of circle and ellipse to the detected boundary of eddy, the results show that the fitting accuracy of ellipse is higher than that of circle.
- mesoscale eddy /
- eddy detection /
- circle fitting /
- ellipse fitting

HTML全文

图 1 涡旋调查站位

红色*表示温盐观测站位，黑线表示ADCP观测航迹

Fig. 1 Survey stations of the eddy

Red * denote the temperature and salinity stations, black lines delineate the track for ADCP observations

下载: 全尺寸图片幻灯片

图 2 涡旋边界的圆拟合（a）和椭圆拟合（b）结果

Fig. 2 Circle (a) and ellipse (b) fitting results of the eddy boundary

下载: 全尺寸图片幻灯片

图 3 涡旋边界（红线）与实测流场（流场为15 m、50 m、100 m和200 m层平均流场）

Fig. 3 The eddy boundary (red line) and observed currents average of 15 m, 50 m, 100 m and 200 m

下载: 全尺寸图片幻灯片

图 4 涡旋边界及其附近15 m (a)、50 m (b)、100 m (c)和200 m (d)层实测流场

Fig. 4 The eddy boundary and the nearby observed currents of 15 m (a), 50 m (b), 100 m (c) and 200 m (d)

下载: 全尺寸图片幻灯片

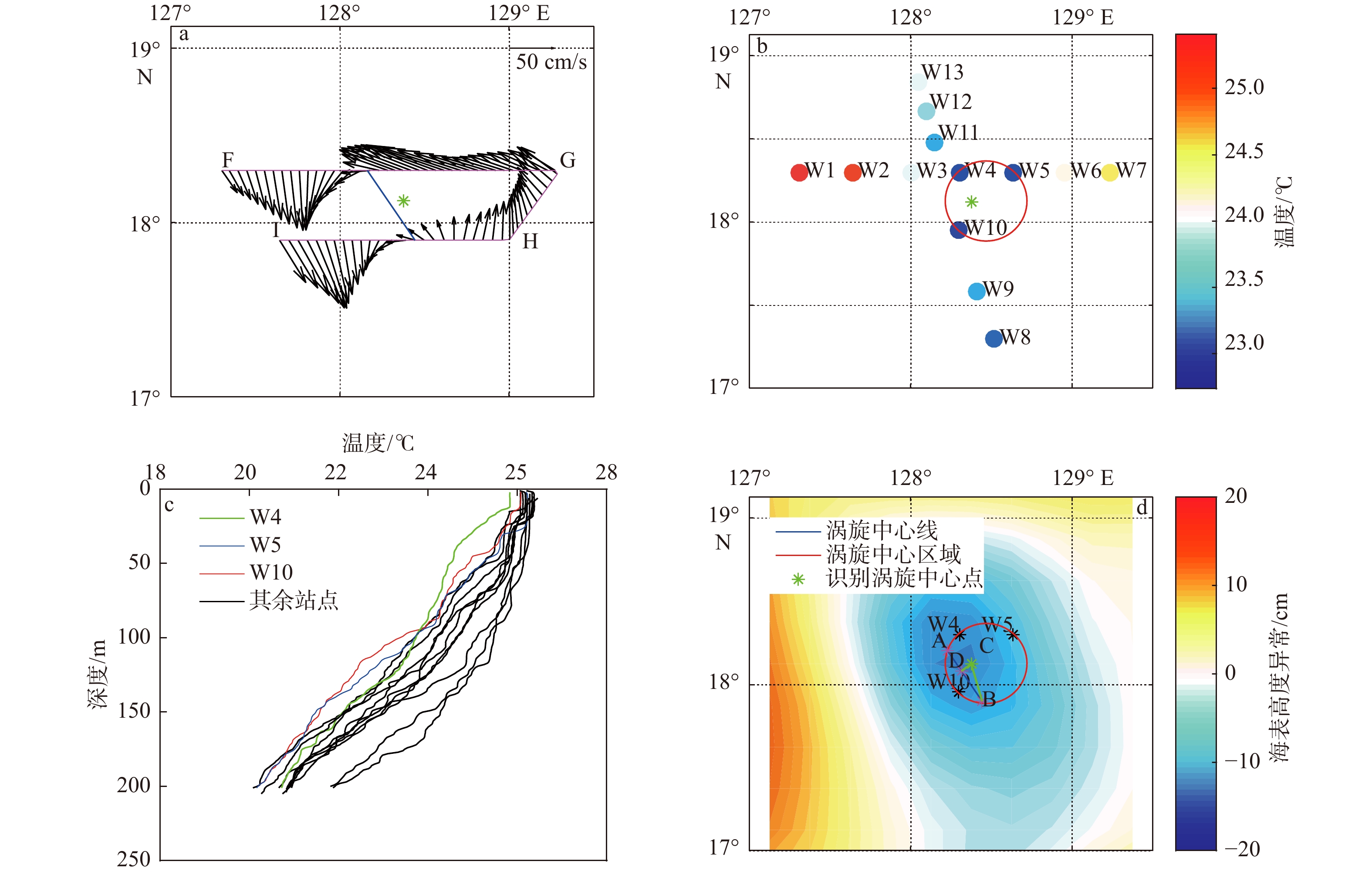
图 5 基于实测数据的涡旋中心位置诊断过程

a. 实测流场确定涡旋中心线（蓝线）；b. 200 m以浅平均温度确定涡旋中心区域（红圈）；c. 观测站点200 m以浅温度剖面图；d. 涡旋中心线和中心区域确定涡旋中心位置范围（线段AB）

Fig. 5 Diagnosis processes of the eddy center based on observed data

a. The line (blue line) passing through the eddy center that diagnosed by observed current; b. the eddy core areas (red circle) determined by temperature that averaged shallower than 200 meters of each profile; c. temperature profiles that shallower than 200 meters of observed stations; d. region of the eddy center (line segment AB) determined by the line and the core areas

下载: 全尺寸图片幻灯片

图 6 边界区域与圆区域叠加

Fig. 6 The eddy boundary overlaps with the circle

下载: 全尺寸图片幻灯片

图 7 单个涡旋边界拟合结果（a）（矢量箭头为地转流）及拟合边界附近地转流分布（b）

Fig. 7 Fitting results of the eddy boundary (a) (vectors indicate the geostrophic current) and the distribution of geostrophic current nearby the fitting boundary (b)

下载: 全尺寸图片幻灯片

图 8 多个涡旋拟合结果（a）及其拟合边界附近地转流分布（b）（Nxx为涡旋编号）

Fig. 8 Fitting results of several eddy boundaries (a) and the distribution of geostrophic current nearby the fitting boundaries (b) (Nxx denote the eddy number)

下载: 全尺寸图片幻灯片

表 1 N01–N09号涡旋圆与椭圆拟合结果（OR、RR和α）

Tab. 1 The results (OR, RR and α) of circle and ellipse fitting for number N01 to N09 eddies

	N01	N02	N03	N04	N05	N06	N07	N08	N09	平均	方差
OR（圆）	0.77	0.86	0.85	0.81	0.85	0.89	0.81	0.86	0.82	0.83	0.001
OR（椭圆）	0.95	0.90	0.88	0.87	0.87	0.92	0.83	0.81	0.88	0.88	0.001
RR（圆）	0.36	0.17	0.24	0.47	0.13	0.16	0.43	0.21	0.24	0.26	0.013
RR（椭圆）	0.09	0.17	0.20	0.29	0.11	0.13	0.11	0.30	0.18	0.17	0.005
α（圆）/（°）	32.8	17.3	27.1	36.0	17.6	14.9	27.4	25.5	31.1	25.5	49.0
α（椭圆）/（°）	10.3	15.4	21.6	23.1	14.1	8.0	15.9	21.2	25.3	17.2	31.0

下载: 导出CSV

参考文献(19)

[1]	Dong Changming, McWilliams J C, Liu Yu, et al. Global heat and salt transports by eddy movement[J]. Nature Communications, 2014, 5: 3294.
[2]	McWilliams J C. The nature and consequences of oceanic eddies[M]//Hecht M W, Hasumi H. Ocean Modeling in an Eddying Regime. Washington: American Geophysical Union, 2008, 177: 5−15.
[3]	Chelton D B, Schlax M G, Samelson R M, et al. Global observations of large oceanic eddies[J]. Geophysical Research Letters, 2007, 34(15): L15606.
[4]	Chelton D B, Schlax M G, Samelson R M. Global observations of nonlinear mesoscale eddies[J]. Progress in Oceanography, 2011, 91(2): 167−216.
[5]	崔伟, 王伟, 马毅, 等. 基于1993−2014年高度计数据的西北太平洋中尺度涡识别和特征分析[J]. 海洋学报, 2017, 39(2): 16−28. Cui Wei, Wang Wei, Ma Yi, et al. Identification and analysis of mesoscale eddies in the Northwestern Pacific Ocean from 1993−2014 based on altimetry data[J]. Haiyang Xuebao, 2017, 39(2): 16−28.
[6]	Okubo A. Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences[J]. Deep Sea Research and Oceanographic Abstracts, 1970, 17(3): 445−454.
[7]	Wesis J. The dynamics of enstrophy transfer in two-dimensional hydrodynamics[J]. Physica D: Nonlinear Phenomena, 1991, 48(2/3): 273−294.
[8]	Sadarjoen I A, Post F H. Detection, quantification, and tracking of vortices using streamline geometry[J]. Computers & Graphics, 2000, 24(3): 333−341.
[9]	Fang Fangxin, Morrow R. Evolution, movement and decay of warm-core Leeuwin Current eddies[J]. Deep Sea Research Part II: Topical Studies in Oceanography, 2003, 50(12/13): 2245−2261.
[10]	Chaigneau A, Gizolme A, Grados C. Mesoscale eddies off Peru in altimeter records: identification algorithms and eddy spatio-temporal patterns[J]. Progress in Oceanography, 2008, 79(2/4): 106−119.
[11]	Yi J, Du Y, He Z, et al. Enhancing the accuracy of automatic eddy detection and the capability of recognizing the multi-core structures from maps of sea level anomaly[J]. Ocean Science, 2014, 10(1): 39−48.
[12]	Wang Guihua, Su Jilan, Chu P C. Mesoscale eddies in the South China Sea observed with altimeter data[J]. Geophysical Research Letters, 2003, 30(21): 2121.
[13]	Chen Gengxin, Hou Yijun, Chu Xiaoqing. Mesoscale eddies in the South China Sea: mean properties, spatiotemporal variability, and impact on thermohaline structure[J]. Journal of Geophysical Research: Oceans, 2011, 116(C6): C06018.
[14]	杨光. 西北太平洋中尺度涡旋研究[D]. 青岛: 中国科学院海洋研究所, 2013. Yang Guang. A study on the mesoscale eddies in the northwestern Pacific Ocean[D]. Qingdao: Institute of Oceanology, Chinese Academy of Science, 2013.
[15]	江伟, 楼伟, 邢博. 中尺度涡自动识别算法比较与应用[J]. 海洋通报, 2016, 35(3): 294−298. doi: 10.11840/j.issn.1001-6392.2016.03.008 Jiang Wei, Lou Wei, Xing Bo. Comparison and application of meso-scale eddy detection algorithm[J]. Marine Science Bulletin, 2016, 35(3): 294−298. doi: 10.11840/j.issn.1001-6392.2016.03.008
[16]	Gander W, Golub G H, Strebel R. Least-squares fitting of circles and ellipses[J]. BIT Numerical Mathematics, 1994, 34(4): 558−578.
[17]	Rosin P L. Ellipse fitting by accumulating five-point fits[J]. Pattern Recognition Letters, 1993, 14(8): 661−669.
[18]	钮毅. 部分遮挡条件下椭圆目标识别[D]. 上海: 上海交通大学, 2007. Niu Yi. Detection of partially occluded ellipses[D]. Shanghai: Shanghai Jiao Tong University, 2007.
[19]	曹芳. 计算机视觉中的各点异性回归技术[D]. 上海: 上海海事大学, 2004. Cao Fang. The heteroscedastic regression technology in computer vision[D]. Shanghai: Shanghai Maritime University, 2004.